Authors:
(1) Anatol Guglielmi, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(2) Boris Klain, Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(3) Alexey Zavyalov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(4) Oleg Zotov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences and Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences.
Table of Links
Abstract: 130 years ago, Omori formulated the first law of earthquake physics. The essence of the law is that the frequency of aftershocks decreases hyperbolically over time. 100 years ago, Hirano doubted the universality of Omori's law and proposed a power law for the evolution of aftershocks. Our paper is devoted to these two outstanding events, which played a significant role in the development of seismology. The paper also contains a brief summary of the modern approach to the construction of a phenomenological theory of aftershocks. Within the framework of the phenomenological approach, the epoch of harmonic evolution of the source, “cooling down” after the main shock, the bifurcation of the source, the cumulative effect of a round-the-world echo, the modulation of global seismicity by spheroidal oscillations of the Earth, mirror triads, migration of aftershocks, and a number of other previously unknown geophysical phenomena were discovered. It is emphasized that the phenomenological theory has been formed in recent years on the basis of a thorough analysis of the fundamental research of the pioneers who laid the foundations of modern seismology.
Keywords: earthquake, aftershock, Omori law, Hirano-Utsu law, source deactivation, proper time, evolution equation.
Introduction
100 years ago, Hirano proposed a power law for the evolution of aftershocks from a strong earthquake [1], having doubted the universality of the hyperbolic law proclaimed by Omori 130 years ago [2]. Before describing these two outstanding events that played a significant role in the development of seismology, we will briefly outline the modern approach to constructing a phenomenological theory of aftershocks [3].
Let us define the earthquake source as a rock mass inside the convex shell of the aftershock envelope. Let us introduce the phenomenological parameter σ (t), which generally characterizes the state of the source at time t . We will call the quantity σ the the source deactivation coefficient. We will assume that the σ value indicates the rate at which the source loses its ability to excite aftershocks. Let us replace t with the so-called proper time as follows:

It is known that the frequency of aftershocks on average decreases over time more slowly than exponentially [4]. Therefore, the choice of a linear equation does not suit us. Let's try to use the simplest nonlinear equation

The choice [5] of the equation with quadratic nonlinearity turned out to be extremely successful. First, the evolution equation (2) allows for interesting generalizations [3, 6]. Secondly, and this is the main thing, it allows a new approach to the processing and analysis of aftershocks.
Let us rewrite (2) in the form

and pose the inverse source problem for equation (3). The essence of the inverse problem is to calculate the deactivation coefficient σ (t) from the aftershock frequency n (t) known from observations [7].
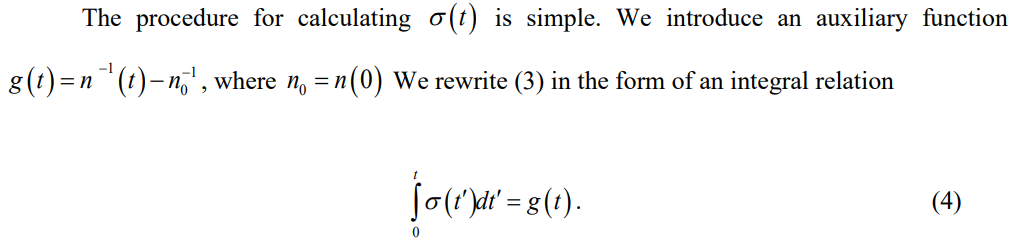
The formal solution to the task is obvious: σ = dg / dt. However, this solution is unstable, since the inverse problem is formulated incorrectly, as is usually the case when setting inverse problems in geophysics. The incorrectness is associated with rapid fluctuations of the function n (t). Regularization in this case comes down to smoothing the auxiliary function. As a result we have

where the angle brackets indicate the smoothing procedure.
Within the framework of the phenomenological approach, a number of interesting geophysical phenomena have been discovered: harmonic evolution of the source [8], source bifurcation [9], cumulative effect of round-the-world echo [10, 11], modulation of global seismicity by free vibrations of the Earth [12], mirror triads and solitary strong earthquakes [13], migration of aftershocks [14].
We emphasize that, following Hugo, we recognize that the new is based on the previous. And we fully understand that the phenomenological theory of aftershocks [3] was formed under the strong influence of the works of the founders of seismology [1, 2].
This paper is available on arxiv under CC BY 4.0 DEED license.

